[4-minute read]

TL;DR. Non-autoregressive (NAR) models generate texts much faster than auto-regresssive (AR) models. However, we find previous NAR approaches, largely developed for Machine Translation, fail harshly when faced with Task-Oriented Dialogue and Data-to-Text. Our NAACL 2024 paper introduces Control-DAG, a constrained decoding algorithm that uses Weighted Finite State Automata (WFSA) to impose regular-expression constraints on NAR text generation. Control-DAG addresses three key limitations in applying NAR models to general Natural Language Generation (NLG): Corrupted entity names, Out-Of-Vocabulary (OOV) generation, and responses that are too brief. Directed Acylic T5, our model, presents the first practical NAR baseline on the Schema Guided Dialogue and the DART data-to-text datasets when decoded with Control-DAG.

Paper: https://arxiv.org/abs/2404.06854
Code: https://github.com/EriChen0615/ControlDAG

NAR Generation: Three Limitations

We are interested in Task-Oriented Dialogue (TOD) Response Generation and Data-to-Text (D2T) Generation. Both take structured data (key-value pairs or triplets) as input with the aim to generate fluent text that accurately conveys the information in the input.

We find three limitations in apply the Directed Acyclic Transformer, a strong NAR model in Machine Translation, to TOD and D2T.

1. Corrupted Entity Name. Misspelt telephone number and names (e.g. Upper Ossington -> Lower Ossington), etc. in up to 40% of the responses.
2. Out-Of-Vocabulary (OOV) Generation such as "Performhanna" and "treee" in over 20% of the responses.
3. Much shorter response compared to the reference response (e.g., "Charles Darwin Christ's College").

NAR systems are unusable in general NLG unless these limitations are addressed: Corrupted entities are mis-information; OOV generations are essentially gibberish; and short responses are often fragmented sentences.

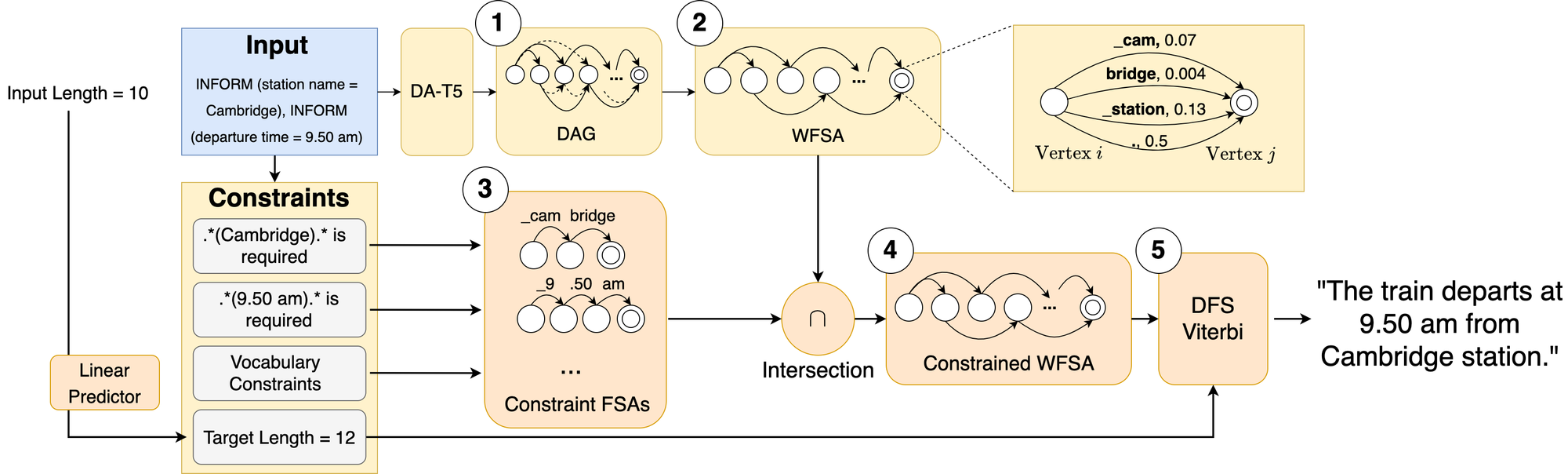
Control-DAG Procedure

Control-DAG is a constrained decoding algorithm designed for Directed Acyclic models, a type of NAR models that generate Directed Acyclic Graphs (DAGs) where each path corresponds to one hypothesis.

We implement three types of constraints:

1. Hard Lexical Constraints: specified words/phrases are guaranteed to appear in the generated text, eradicating entity names corruption.
2. Vocabulary Constraints: ensure all generated words are from a prescribed dictionary, eliminating OOV generation.
3. Lenght Constraints: a length target can be specified.

We express lexical and vocabulary constraints as regular expressions and build their equivalent Finite State Automata (FSA). To find hypotheses that satisfy all constraints, we convert the DAG to Weighted Finiate State Automata (WFSA) and perform intersection with the FSAs. This yields a WFSA that only contains constraint-satisfying hypotheses. To control generation length, we use a modified Viterbi algorithm to find path with a given number of edges in the WFSA.

Task-Oriented Dialogue and Data-to-Text Results

We validate Control-DAG on the Schema Guided Dialogue (SGD) dataset for TOD and the DART dataset for D2T. We train our Directed Acyclic T5 model from scratch on the respective datasets.

We report BLEURT for quality, BLEU's Brevity Penalty (BP) for text length. Smaller BP means shorter generation. Neologism (NEO) for proportion of generations containing at least one OOV error, Slot Error Rate (SER) and Exact Occurrence Error Rate (EOR) for corrupted entity names on the SGD and DART, respectively. A slot/exact occurrence error occurs when a specified entity is not reproduced exactly.

Speed up (Spd. Up) is measured against Autoregressive Constrained Beam Search (CBS) which guarantees zero SER/EOR. We emphasize that zero SER/EOR is necessary for practical system, as even a small error rate will result in a large number of false information in real services.

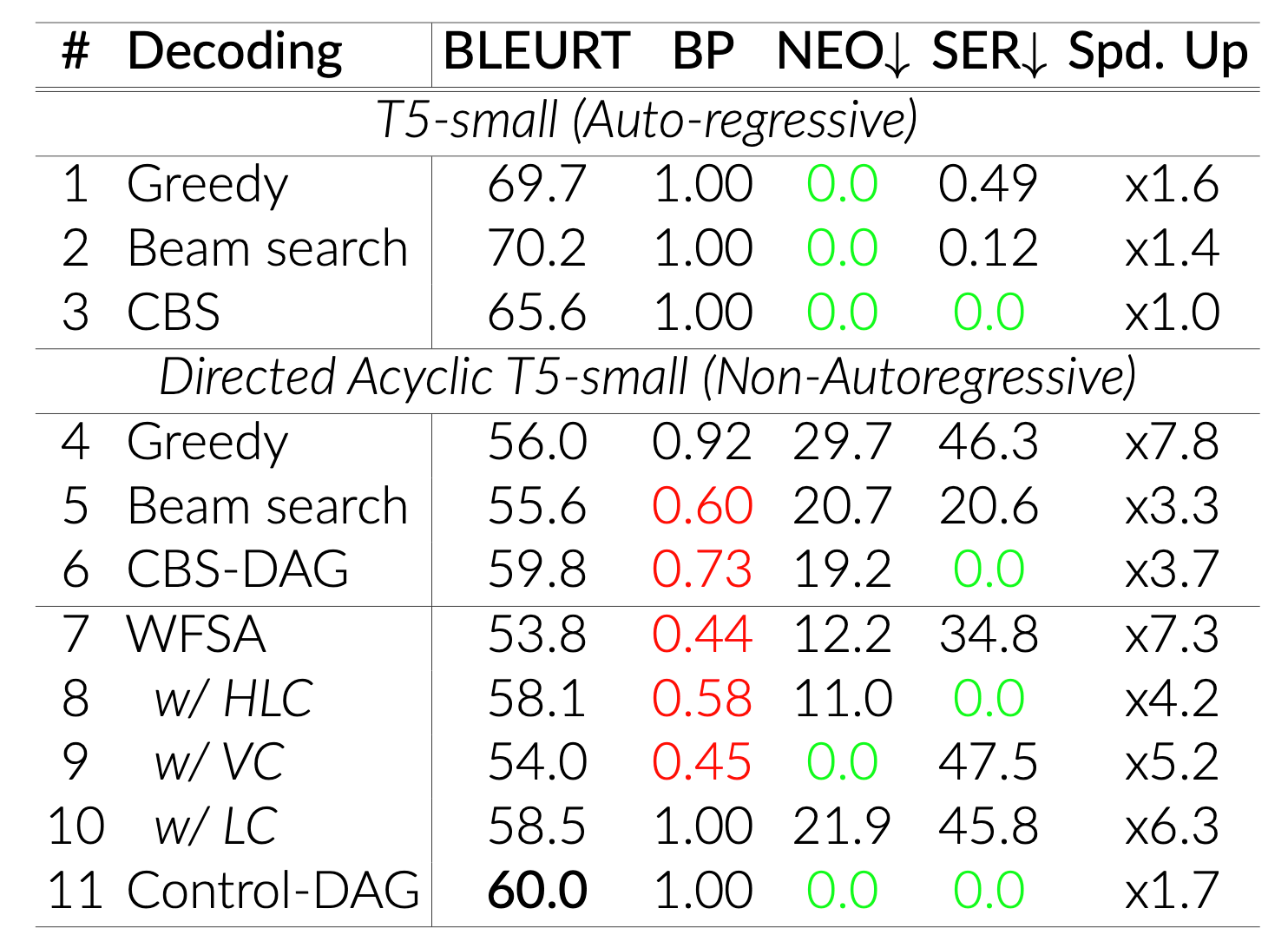
Row 8, 9, 10 show that our decoding constraints work individually: Hard Lexical Constraint (HLC) eliminates SER; Vocabulary Constraints eliminates OOV errors; and Length Constraint (LC) leads to better text lengths (BP=1.0). Row 11 (Control-DAG) combines them, achieving overall best NAR performance. CBS-DAG (Row 6) is auto-regressive CBS adapted for NAR Directed Acyclic model.

Conclusion

We propose Control-DAG for decoding NAR Directed Acyclic models with lexical, vocabulary, and length constraints. Constrained decoding is efficiently perfromed via well-studied WFSA algorithms. Directed Acyclic T5 with Control-DAG establishes strong NAR results on the SGD and DART datasets.

Find out other works from me: https://www.jinghong-chen.net/tag/my-work/.