Executive Summary: LoRA (Low-Rank Adaptation) fine-tunes a low-rank weight update matrix instead of the whole weight matrix. MultiLoRA modifies LoRA to better learn multiple tasks simultaneously. A MultiLoRA module can be viewed as several LoRA modules connected in parallel and weighted by learnable scaling factors. Finetuning LLaMA with MultiLoRA enhances performance on a curated multi-task benchmark compared to finetuning with LoRA. Additionally, the singular values of the learned weight update matrix from MultiLoRA fine-tuning are more balanced than that from LoRA. The authors argue that this “democratization” of weight update subspaces underpins MultiLoRA's effectiveness in multi-task learning. Paper.

LoRA Refresher

Assume a pre-trained weight matrix \(W_0\in R^{d\times k}\). In LoRA, the layer activation \(h\) is given by \(h=W_0 x + \Delta W x = W_0 x + BA x\). \(\Delta W\) is the weight update matrix approximated by matrics \(A\) and \(B\) whose rank \(r \ll min(d,k)\). \(\Delta W\) can also be viewed the outer-product of \(A\) 's and \(B\) 's row/column vectors. \(B\) is initialized with all zeros. \(A\) is initialized from a normal distribution.

MultiLoRA

SVD analysis shows that the weight update matrix from LoRA-tuning is dominated by a few principal components with high singular values, whereas the weight update matrix from standard fine-tuning has more balanced singular values. This motivates MultiLoRA to balance (demoratize) subspace components.

MultiLoRA uses multiple regular LoRA modules to approximate each weight matrix. These LoRA modules are connected in parallel. The final output is the weighted sum of all LoRA modules' output. The weight (\(scaling_{1,...,n}\) in the figure) of each LoRA module is learned during fine-tuning.

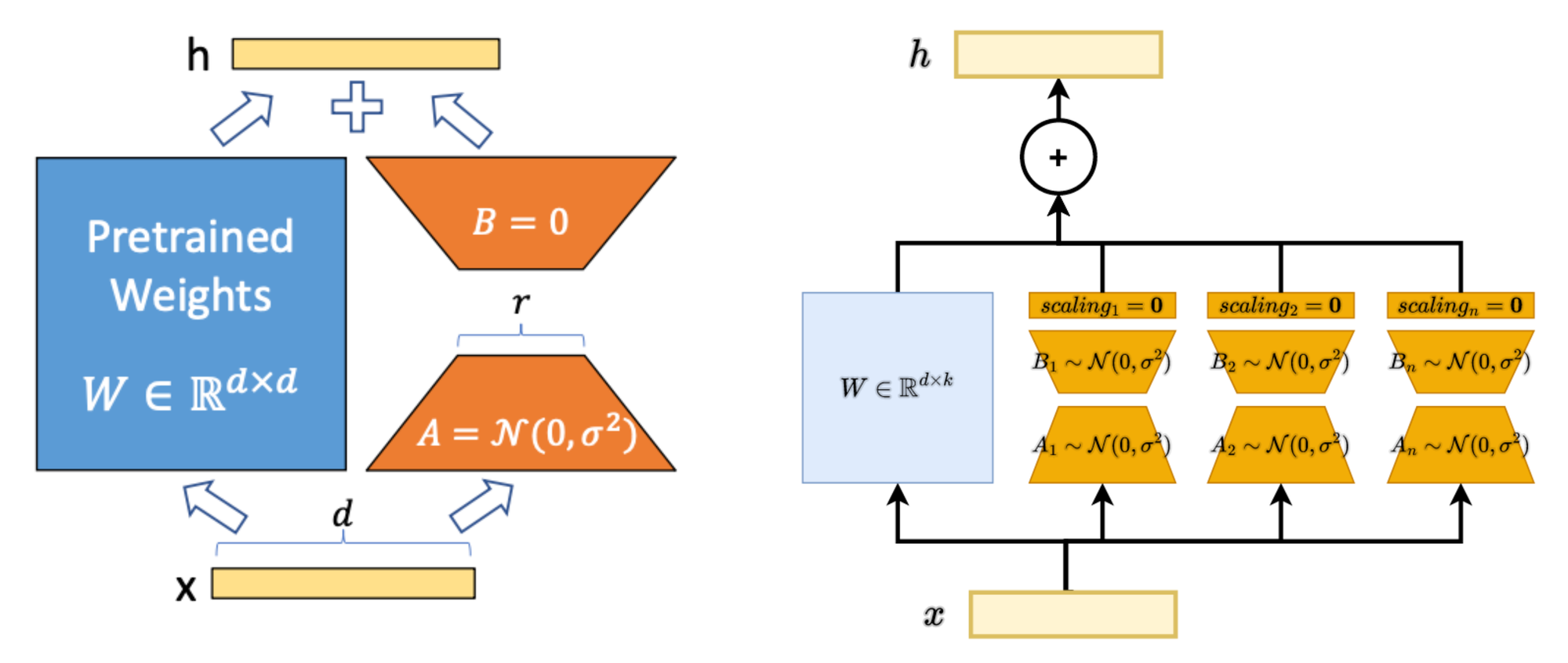
The parameters of \(B\) are initialized from a normal distribution such that the output after ReLU activation has a variance of 1 (Kaiming-Uniform). Scaling factors are zero-initialized. This ensures identical output at training step 0 as the untrained model.

Experiments and Analyses

The authors build a multi-task dataset for generative Large Langauge Models which encompasses Alpaca for instruction following, MMLU for world knowledge, GSM8K for arithmetic reasoning and SuperGLUE for NLU. For training, they fine-tune LLaMA on this mixture dataset using standard fine-tuning (FT), LoRA, and MultiLoRA. The same number of ranks (96 or 160) are used for LoRA and MultiLoRA. For evaluation, they report average accuracy on MMLU (Massive Multitask Language Understanding), Boolq (Boolean Questions) , MultiRC (Multi-Sentence Reading Comprehension), RTE (Recognizing Text Entailment), and WiC (The Word-in-Context Dataset).

Here are the key findings:

• MultiLoRA consistently outperforms LoRA in multi-task learning across a range of base model parameter sizes (7B-65B).
• Smaller models gain more from MultiLoRA when compared to their LoRA counterparts (6B: +2.7 avg accuracy; 65B: +0.4 avg accuracy).
• MultiLoRA is only slightly worse than full-parameter fine-tuning in complex multi-task learning scenarios. The gap widens for larger base model (up to 0.3 avg accuracy with LLaMA-65B).
• In the single dataset setting, MultiLoRA performs similarly as LoRA and full-parameter fine-tuning.
• MultiLoRA has similar throughput as LoRA, but requires higher peak GPU memory (VRAM) in training than LoRA.

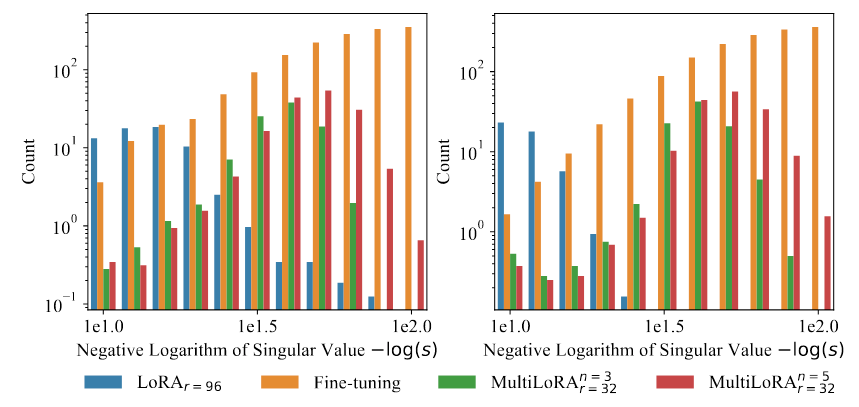
Figure 2 is a singular values histogram obtained from performing SVD on the weight update matrics for key projection and value projection. Note that the singular values from regular fine-tuning (in Orange) are "balanced" in the sense that most subspaces have similar singular values. However, fine-tuning with LoRA (in Blue) induces a few dominating subspaces with high singular values. MultiLoRA (in Green and Red) yields more balanced singular values than LoRA. The authors attribute better multi-tasking ability to this democratizion of subspaces.

Concluding Thoughts

I view MultiLoRA as a straight-forward variant of LoRA which uses several LoRAs in parallel to obtain the low-rank weight update. The paper is well-motivated and backed by extensive experiments with multi-tasking LLM, but the presentation is inflated.

Another common multi-tasking strategy is to first individually fine-tune models on a single task (with or without LoRA) and then merge the weights to obtain one multi-tasking model. This is known as Task Arithmetic. This paper at NeurIPS 2023 investigates why Task Arithmetic works and how to make it better. I plan to write another post on that. If you have any question, let me know in the comment.